![]()
(a) Solve for the bound state energies and wavefunctions. Consider the
cases W > 0 and W< 0 separately. [Hint: Integrate the Schrödinger\
equation between ![]() and
and ![]() . Let
. Let ![]() and
note that the derivative of the wave function is discontinuous at x =
0.]
and
note that the derivative of the wave function is discontinuous at x =
0.]
(b) In the case of E > 0 (where E is the energy), obtain the
reflection coefficient R and transmission coefficient T. Write the
coefficients in terms of the dimensionless parameter ![]() where
where ![]() is the ground state energy obtained in part (a), in the
case of W > 0. What is the behavior of T(b) as
is the ground state energy obtained in part (a), in the
case of W > 0. What is the behavior of T(b) as ![]() ?
?
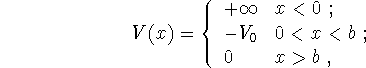
where ![]() and b are positive constants.
and b are positive constants.
(a) Find ![]() as a function of b such that there is just one bound
state, of about zero binding energy, for a particle of mass M.
as a function of b such that there is just one bound
state, of about zero binding energy, for a particle of mass M.
(b) Applying this crude model to the deuteron (a bound state of a
proton and a neutron), evaluate ![]() in MeV, assuming
in MeV, assuming ![]() cm and
cm and ![]() , (where
, (where ![]() is the proton mass).
is the proton mass).
(c) Why did I set ![]() rather than
rather than ![]() in part (b)?
in part (b)?
![]()
where q is positive. You could attempt to solve the Schrödinger equation directly, but the resulting differential equation is quite complicated, (but see e.g. S. Flügge, Practical Quantum Mechanics, problem 39). Instead, you can go through the following tricks which make the solution of this problem quite simple.
(a) Define the differential operator
![]()
Show that the Hamiltonian for this problem can be written in operator form:
![]()
where ![]() is the adjoint of A. Prove that the energy
eigenvalues must be non-negative.
is the adjoint of A. Prove that the energy
eigenvalues must be non-negative.
(b) Construct a second Hamiltonian ![]() given by:
given by:
![]()
Evaluate ![]() explicitly and show that the corresponding potential
is independent of x. Solve for the energy eigenfunctions and
eigenvalues of
explicitly and show that the corresponding potential
is independent of x. Solve for the energy eigenfunctions and
eigenvalues of ![]() . What is the minimum value of the allowed
energy eigenvalues?
. What is the minimum value of the allowed
energy eigenvalues?
(c) Show that if ![]() is an eigenfunction of H, then
either:
is an eigenfunction of H, then
either:
(i)is an eigenstate of
, or
(ii)
is an eigenstate of H with zero eigenvalue.
Similarly show that if ![]() is an eigenstate of
is an eigenstate of ![]() then
then
![]() is an eigenstate of H. Conclude that H and
is an eigenstate of H. Conclude that H and
![]() have the same eigenvalue spectrum, except for one
eigenstate of H with zero eigenvalue.
have the same eigenvalue spectrum, except for one
eigenstate of H with zero eigenvalue.
(d) Let ![]() be an energy eigenfunction of H with energy
be an energy eigenfunction of H with energy ![]() , with k > q. Define
, with k > q. Define ![]() .
Then
.
Then ![]() takes the form:
takes the form:
![]()
Using results of parts (b) and (c), write down the exact energy eigenfunctions of H with k > q. Then determine the reflection and transmission amplitudes R(K) and T(K).
(e) Check for conservation of probability ( ![]() ). Using
the expression for T, find all the bound state energies of H.
). Using
the expression for T, find all the bound state energies of H.
(f) Using part (c), show that if ![]() is the ground state of H
with zero eigenvalue, then
is the ground state of H
with zero eigenvalue, then ![]() . Solve the resulting
differential equation (in the coordinate basis) for the ground state
wave function of H.
. Solve the resulting
differential equation (in the coordinate basis) for the ground state
wave function of H.
(a) Show that the translational operator ![]() commutes withe the Hamiltonian:
commutes withe the Hamiltonian:
![]()
(b) We may choose the energy eigenstates to be simultaneous eigenstates of the translation operator. Show that the general form of such eigenstates is:
![]()
where ![]() . That is, the eigenfunctions are plane
waves modulated by a function with the periodicity of the potential.
(This is called Bloch's theorem).
. That is, the eigenfunctions are plane
waves modulated by a function with the periodicity of the potential.
(This is called Bloch's theorem).
(a)where.
(b)
.
(c)
,
(a) Obtain the probability for finding the electron in the ![]() state as a function of time.
state as a function of time.
(b) Find the expectation value of ![]() as a function of time.
as a function of time.
(c) Check explicitly the extreme cases of ![]() and
and ![]() .
.